2. DIRECT ACTION OF IONISING RADIATION
2.1. Radiation Sensitivity
The chemical and biological effects of ionising radiation originate from two basic types of interactions. In direct action the radiation energy is deposited directly in targets. Indirect action refers to absorption of energy by the external medium, leading to the production of diffusive intermediates which then attack the targets. The "dilution effect" distinguishes between direct and indirect action. Consider a medium containing C0 target entities per unit volume. In direct action, the damaged fraction of entities C*/C0 does not depend on C0 because the total energy absorbed by the entities increases linearly with increasing C0. For indirect action, C*/C0 decreases with increasing C0 because the energy absorbed by the medium is independent of C0. (These predictions fail at very high C0. ) Both direct and indirect action may contribute to radiation damage at the cellular level. The effect of ionising radiation on a biological system is quantified by the radiation sensitivity (S), which is defined as the reciprocal of the radiation dose required to cause a certain fractional change in a selected property. 1/D37 is frequently employed as measure of radiation sensitivity, where D37 is the radiation dose at which approximately 63% of the starting entities have acquired the specified damaged. Various factors may contribute to radiation sensitivity at the cellular level, including the specific biological function that is affected, the type or "quality" of the radiation, ambient conditions, presence of agents that sensitize or protect against radiation damage, and cellular repair processes. Cell cycle, dose rate, and dose fractionation are additional determinants of mammalian cell radiation sensitivity. Radiation damage in higher animals is defined in terms of LD50, which is the radiation dose which has a 50% chance of lethality.
For humans exposed to whole body gamma-rays, LD50 is about 5 Gy.Conservation of energy is the key principle controlling the interactions of ionizing radiation with matter. For example, ejection of an electron from an atom by an x-ray requires a photon energy at least as large as the binding energy of the electron. However, the net effect is more complicated because the excess kinetic energy of the ejected electron and recoil ion are dissipated at later times and different locations. There is no comprehensive theory of radiation interactions owing to the multiplicity of possible effects. Instead, a number of different mechanisms are cobbled together in order to give an overall view. An elegant theoretical approach to direct action of fast electrons is based on concepts of molecular photophysics. An isolated molecule experiences an electric pulse when a fast electron flies past it. It can be shown that the transfer of energy from the electron to the molecule is equivalent to bombarding the molecule with a stream of
"virtual photons", whose energy varies from zero to a maximum of hV/b, where V is the electron velocity and b is the distance of closest approach. For example, the maximum virtual photon energy is about 1200 eV for a 0.5 MeV electron passing 1 nm from a molecule. The detailed theory shows that the number of virtual photons possessing a given energy is inversely proportional to that energy. Each interaction transfers less than 0.02% of the initial energy of the fast electron. However, the energy range of the virtual photons is ample to induce electronic transitions. Molecular measurements in the gas phase have led to detailed information about the excitation properties of atoms and molecules which can be utilized for quantitative calculations. Elementary radiation theory shows that the number of molecules raised to a given state of excitation is proportional to fe /e, where e is the energy of the optical transition and fe is a number proportional to the probability that the absorption of a photon by the molecule induces the given transition; fe is termed the oscillator strength of the transition. The ionization potential of most atoms and molecules in the gas phase is the order of 10-15 eV, e.g., H, 13.6 eV; O2, 12.1 eV; CH4, 12.7 eV; C6H6, 9.2 eV. Accordingly, the higher energy virtual photons are expected to induce ionisations while low energy virtual photons induce electronic excitations. Allowed (i.e., highly probable) optical transitions take place in 10-16 - 10-15 s which is a short time compared to the period of molecular vibrations, which is 10-14 - 10-13 s. Thus, the primary excitation act is relatively unaffected by the environment of the molecule and the basic features of the excitation process in a condensed phase are expected to be similar to the gas phase. The fate of the secondary radiation products may be quite different in a condensed medium. This theory provides information about energy transfer from fast primary and secondary electrons and secondary electrons generated by energy transfer from x-rays, gamma-rays, and heavy charged particles. Information about the primary interactions of heavy particles and EMR derives from energy loss theory as developed in nuclear physics.2.2. Energy Loss by Charged Particles
A heavy charged particle (e.g., proton, deuteron, alpha ) loses kinetic energy via a sequence of small energy transfers to
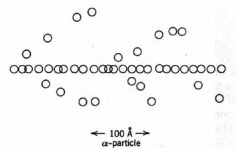
Figure 6. Spurs and excitations in the track of an alpha-particle in water. Each circle depicts an ionisation or excitation event. The branching tracks are "delta rays". (Adapted from Spinks and Woods.)
atomic electrons in the medium. Most of the energy deposition occurs in the infratrack, a narrow region around the particle track extending about 10 atomic distances. Ionization outside the infratrack is caused by very energetic particles that escape from the infratrack and secondary electrons. The more energetic interactions eject electrons from their parent atoms and generate primary ion-pairs. An approximate expression for the maximum energy transfer to an electron from a heavy charged particle of mass number A and energy E (MeV) is given by:
(1)
: Wmax = 215 E /Awhere Wmax is in eV. Thus, the secondary electrons generated by a 5 MeV alpha particle range up to about 300 eV of kinetic energy. The more energetic secondary electrons can initiate additional ionisations, while less energetic secondary electrons induce electronic excitations. The lowest energy secondary electrons are referred to as "sub-excitation", whose role in biological radiation damage remains unclear. Since only a small fraction of the initial energy is transferred at each event, a track consisting of clusters of ions or spurs is generated along the path of the moving particle. Most spurs in water comprise 1-5 ion-pairs. These tracks may be visualized in a cloud chamber by their vapor trail. High-energy secondary electrons are occasionally generated. Energy loss by these energetic electrons leads to short branching tracks or
"delta rays" (Fig. 6). Delta rays may terminate in larger pear-shaped regions of ionisation or "blobs". Similar considerations apply for energy transfer to a fluid medium in indirect action.The energy loss per unit length of particle track is termed the stopping power in nuclear physics and linear energy transfer (LET) in radiation biology. Heavy charged particles are referred to as "high LET radiation" while x-rays, gamma-rays, and fast electrons are "low LET radiation". The dependence of LET on the energy and electric charge of the flying particle was developed by Bethe and Bloch. The approximate result for a non-relativistic heavy charged particle of kinetic energy E and charge z is:
(2)
: LET . (z2 Ne/E) Loge (4E/I)where Ne is the number of electrons per unit volume in the medium and I is the average ionisation potential of the molecules in the medium. The ionization potential of an atom is about 14Z eV
. An average value is employed for molecules, e.g., for water I . 14 [(2 x 1) + (1 x 8)]/ 3 = 47 eV. A more exact expression is: I/Z = 9.2 + 4.5Z –2/3. An alpha particle emitted by 226Ra88 travels about 33 mm in water and has an average LET of 145 keV/mm. Equation (2) shows that the ionization density along the track increases as the particle slows down (Fig. 7). Eventually,| Ionising Radiation | Mean range in water (mm) | Average LET (keV/m) |
| 228Ra alpha (4.8 Mev) | 0.033 | 145 |
| 3 MeV proton | 0.072 | 42 |
| 3 MeV electron | 15 | 0.20 |
| 90Sr beta (0.544 MeV max) | 1.8 | 0.30 |
| 60Co gamma (1.33, 1.17 MeV) | 100 | 0.2 |
Table 3. Penetration in water and average LET of some ionising radiation
.the charge on the flying particle is neutralized by capturing electrons from the medium after which the rate of ionisation decreases rapidly. An ionisation maximum near the end of a charged particle track is the Bragg peak. The Bragg peak has been utilized in radiation therapy of cancer to localize the maximum radiation effect within the irradiated tissue instead of at the surface. The approximate range (R) of a heavy charged particle is given by:
(3)
: R = CE0nwhere E0 is the initial energy. Integration of Eq. (1) leads n = 2. Experimental data show that n depends on the particle
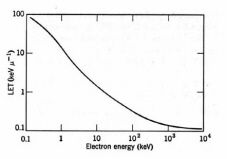
Figure 7. Average LET for electrons in water. (Adapted from Spinks and Woods.)
and the medium. For protons in air n = 1.75.
Table 3 summarizes thesome LET values in water. The track-average values of LET are calculated by dividing the initial energy by the penetration depth. More sophisticated calculations have been employed with a cutoff at the minimum ionisation energy.Fast electrons lose energy by inelastic collisions with electrons of the medium. The number of electrons in an incident beam of mono-energetic electrons decreases with increasing depth, while the density of ionisation attains a maximum in a region between the front surface and the maximum penetration depth. A typical fast electron track is depicted in
Fig. 8. Electrons tracks are less dense than the tracks of heavy charged particles, owing to the lower LET, and the spurs are more widely spaced with more frequent delta rays terminating with blobs. The theoretical expression for LET of non-relativistic electrons is the same as Eq. (2), except the expression inside the natural logarithm is one-fourth as large. In the case of beta emitters, only
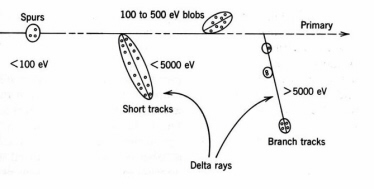
Figure 8. Distribution of ion-pairs and excitations in the track of a fast electron in water (not to scale). (Adapted from Spinks and Woods.
)about 20% of beta particles penetrate to the maximum range owing to their broad energy distribution. In addition to energy deposition, electrons undergo elastic electron-electron collisions leading to multiple scattering and curvature of the tracks which complicate the dosimetry in extended sources. In water, the maximum absorbed dose is reached at about 0.8 mm depth for 0.5 MeV electrons, 1.5 mm for 1 MeV electrons, and 5 mm for 3 MeV electrons (Fig. 9).
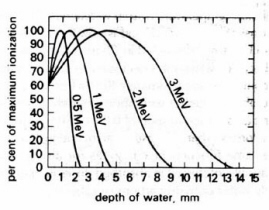
Figure 9. Distribution of dose with depth for fast electrons in water. (Adapted from Swallow.)
2.3. Energy Loss by Electromagnetic Radiation
Unlike fast electrons, a high-energy photon loses a significant amount of energy at each interaction. The depletion of a monochromatic photon beam of fluence rate I(z) traversing a depth z is given by:
(4): I(z) = IoExp(-mattz)
where
matt is the linear attenuation coefficient. The reciprocal 1/matt is the distance in which the intensity of a narrow beam of monochromatic x-rays or gamma-rays decreases by approximately 63%. Unlike heavy charged particles and fast electrons, the maximum dose is delivered by a narrow x-ray beam at the front surface of an absorber. The specific interactions that contribute to matt depend on the medium and photon energy. The photoelectric effect dominates at relatively low photon energy energies. In the photoelectric effect a photon is absorbed and an electron is ejected from the target atom. The outer K-shell energies are relatively low for "low-Z" materials, e.g., about 500 eV for the water molecule. High-Z materials emit more energetic secondary electrons, e.g., about 70 kev for tungsten.For photons of sufficient energy, an electron in the K-shell is ejected about 80% of the time and 20% of the photons interact at the innerL-shell. The "hole" in the L-shell is filled by an electron from the K-shell accompanied by the emission of a "soft" x-ray photon. The secondary photon is absorbed by another photoelectric event in a different atom or in the same atom; the latter process is the Auger effect.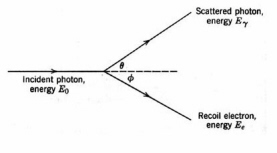
Figure 10. The Compton effect
. The scattered photon may initiate additional events.Photoelectric emission is most efficient for low-energy photons. The Compton effect
is a competing energy loss mechanism in which a photon undergoes inelastic scattering by an atomic electron. Only part of the photon energy is transferred to the electron and the resultant lower-energy photon is scattered (Fig. 10). Compton scattering is significant in low-Z materials over a wide range of photon energies, e.g., about 30 keV to 20 MeV in water and they dominate in high-Z materials at photon energies from at photon energies from 1-5 MeV. Very high-energy photons lose energy by pair production (Fig. 11). In pair-production, the interaction of a photon with the strong electric field of a high-Z nucleus creates an electron and a positron. The minimum photon energy for pair production is the energy equivalent of twice the rest mass of the electron, which is 1.02
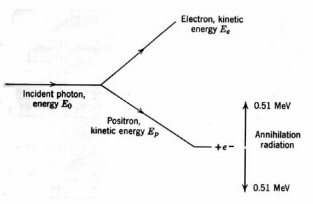
Figure 11. Pair production
.MeV. The two newly created particles lose energy by collisions with atoms of the medium. A thermalized positron may be trapped in the electric field of an electron of opposite spin, forming the hydrogen-like species positronium. Positronium decays after about 0.1 ns by forming two 0.51 MeV "annihilation" photons emitted in opposite directions. Overall, pair production leads to energetic secondary electrons and 0.511 MeV photons. The efficiency of pair production increases with photon energy above 1.02 MeV and is very nearly proportional to Z. The
absorption coefficient for photoelectric emission and Compton scattering in water are equal at approximately 50 keV, above which Compton scattering dominates until about 2 MeV when pair production starts to contribute and equals Compton scattering at 100 MeV.Coherent (energy conserving) scattering of photons does not contribute to energy loss, although it affects the photon distribution and, therefore, it is significant for radiation dosimetry. Biological effects are adequately described by a defining the total absorption coefficient
(ma) and a coherent scattering coefficient (msc) such that:(5)
: matt = ma + mscFor example, 47% of the energy carried by 60Co gamma-rays (1.25 MeV) is lost out of the incident beam after traversing 10 cm of water, of which 22% is absorbed and 25% is scattered. Experimental depth-dose curves for x-rays and gamma-rays depend on the beam geometry. The average track length for a highly collimated beam of x-rays or gamma-rays equals 1/
matt for measurements with a small, on-axis detector. The attenuation of a broad photon beam is more complicated because scattered photons can contribute to the local density of photons and secondary electrons. Experimental measurements show that the density of secondary electrons builds up to a maximum within the irradiated surface and then falls off exponentially deeper into the medium.2.4. Energy Loss by Neutrons
Neutrons are uncharged nuclear particles having A = 1 and a free decay half life about 13 min. The most important property of neutrons in the context of radiation biology is that they interact with atomic nuclei and not with electrons. The efficiency of this interaction depends on the neutron energy and the target. Neutron energies are categorized as "fast" (10 keV-10 MeV), "intermediate" (0.5-10 keV), and "thermal" (
. 0.025 eV). Fast neutrons transfer energy to light nuclei by "billiard ball" elastic collisions. Materials high in hydrogen and deuterium are favored for slowing down of neutrons because a higher fraction of the neutron kinetic energy is transferred to a lighter target. The average number of collisions required to reduce a 2 MeV fast neutron to thermal energies is about 18 in liquid hydrogen, 90 in beryllium, 114 in graphite, and about 2000 in lead. In biological materials 85-95% of the energy of fast neutrons is transferred to hydrogen nuclei leading to recoil protons. Certain nuclei have a high cross section for capturing slow neutrons. This process leads to a compound nucleus. The compound nucleus may be formed in an excited state and return to the lowest energy stateElement |
Scattering cross section (barn) | Absorption cross section (barn) |
| H | 38 | 0.33 (n,g) |
| C | 4.8 | 0.0032 (n,g) |
| N | 10 | 1.75 (n,p) 0.13 (n, g) |
| O | 4.2 | 0.0002 (n,g) |
Table 4. Slow neutron scattering and absorption cross sections by atoms in biological materials in their natural abundance.
by emitting a proton or a gamma-ray.
Table 4 gives the scattering and absorption cross sections for reactions of thermal neutrons with light elements in their natural abundance. The unit of cross section in this table is the barn; 1 barn = 10-24 cm2. (This unit originated from the concept of hitting the side of a barn with a projectile.) The (n,g) reaction of neutrons with H atoms generates 2.2 MeV gamma-rays and the (n,p) reaction with N atoms generates 660 keV protons. Most of the damage in biological materials from slow neutrons results from the secondary protons and gamma-rays emitted by H atoms and N atoms.Next part - TARGET THEORY