A POSSIBLE WAY FOR QUANTIFICATION OF SPIN TRAPPING IN BIOLOGY

Dezsô Gál

Institute of Chemistry. Chemical Research Center, Hungarian Academy

of Sciences, Pusztaszeri út 59-67, Budapest 1025, Hungary

It is well known from the corresponding literature [1-3] that analysis of free radicals in biological samples meets serious difficulties mainly because of their very small steady state concentrations and consequently spin trapping procedures (STP) offer a good possibility for such purpose.

STP is based on the interaction of spin traps (ST) with free radicals (Rad^.) forming a radical adduct (A^.) being more stable than Rad^. and thus accumulating in higher concentrations :

ST + Rad^. ® A^. (1)

Due to the enhanced concentration of A^. compared to Rad^. , in principle, the original radical becomes measurable e.g. by ESR method.

Beyond any doubts STP is very useful if the problem to be solved needs qualitative proof about the role of free radicals supported by different structures of the ESR spectra of the adduct depending on the structure of the parent radical, but problems arise if quantitative data are needed. The reason for this is the fact that the most appropriate ST-s yield only relatively stable adducts which undergo further reactions and therefore the steady state concentrations of [Rad^.] calculated is not accurate and even worst, their changes measured, e.g. in the course of photodynamic effects, are unreliable [4-5].

Therefore it is not by chance, that in many laboratories great efforts have been done to synthesize new ST-s yielding more stable adducts.

It is suggested that certain special experimental runs would enable to deduce data leading to reliable quantitative results for free radicals by STP.

With respect to the [A^.] values it can be written :

(2)

where the second member of the right side corresponds to the radical induced decomposition of the adduct, the third and fourth one its monomolecular and bimolecular decomposition, respectively.

If the kinetics of accumulation of [A^.] is measured directly, we obtain the left side of equ. (2) and in case the experimental arrangement ensures to stop the formation of radicals at various reaction times, its consumption gives the sum of the third and fourth members on the right side for various [A^.]-s.

At the same time, measuring the initial rate of the accumulation of A^. , its consumption can be neglected, that is :

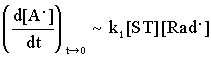(3)

Consequently, the second member of the right side in equ. 2 , that is, the radical induced consumption of the adduct can be calculated.

In addition the value of k₁ can be also determined. Namely, the consump-tion rate of ST, , is equal to the initial rate of the formation (or accumulation) of A^. at the initial stages of the overall process, provided ST reacts exclusively with radicals :

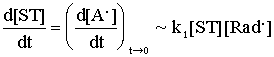(4)

For chain reactions with quadratic combination of the radicals the rate of accumulation of native free radicals :

d[Rad^.] / dt = Wi - k₁[ST][Rad^.] - k_i [A^.][ Rad^.] - k_t [Rad^.]² = 0 (5)

where W_i refers to initiation.

By assuming that at very low conversions the rate of the induced decomposition of the adduct is negligible equations (4) and (5) give:

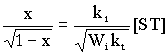(6)

where x (d[ST]/dt) / W_i . [6-7]

Naturally, in order to calculate k₁, the values of the rate of initiation and the rate constant of the radical combination are necessary. By measurements in the presence of different amounts of ST_o and using the initial rates of the formation of the adduct, equ. (6) yields the corres-ponding rate constant k₁ .

Experiments in chemical model systems and at in vitro conditions are under way and numerical results will be described later.

The author expects critical comments concerning above approach.

Finally, comments on the importance of spin trapping for photobiology. Photoinitiation of free radicals in live tissues; effect of antioxidants; studies on Photodynamic Therapy [8-9]; chemiluminescence approach of biological processes all require the knowledge of free radicals in living cells quantitatively rendering the development of STP desirable.

REFERENCES

1.) Edward G. Janzen, L.Anderson Evans, Yasutaka Nishi : J. Amer. Chem. Soc. 94 , 8236-8238, 1972

2.) Georg Buettner, Larry W. Oberley : Biocheem. Biophys. Res. Commun. 83, 69-74, 1978

3.) D.Griller, K.U.Ingold : Acc. Chem. Res. 13, 317-323, 1980

4.) T. Shulyakovskaya, L. Sümegi and D.Gál : Biochem. Biophys. Res. Commun.195; 581-587; 1993

5.) Dezsô Gál, Tamás Kriska, Elena Maltseva : Biochem. Biophys. Res. Commun., 233, 173-176, 1997

6.)N.M.Emanuel, E.T.Denisov, Z.K.Maizus : Oxidation Chain Reactions of Hydrocarbons in Liquid Phase („Nauka", Moscow, 1965, in Russian)

7.E.T.Denisov, A.L.Alexandrov : Zh. Fiz. Khim. 38, 491, (1964)

8.) T.Kriska, Elena Maltseva and D.Gál :. Biochem. Biophys. Res. Commun., 223, 136-140, 1996

9.) Dezsô Gál, Tamás Kriska, Elena Maltseva : Biochem. Biophys. Res. Commun., 233, 173-176, 1997